10. Derivatives and Tangent Lines
b. Tangent Lines
The primary application of a derivative is to find the equation of the tangent line at a point, \(x=a\), on the graph of a function, \(y=f(x)\). The most general line has the standard equation: \[ Ax+By=C. \] The line is vertical if \(B=0\) and non-vertical if \(B\ne0\). Assuming it is not vertical, we can solve for \(y\) and put the equation into slope-intercept form: \[ y=mx+b \qquad (1) \] where \(m\) is the slope and \(b\) is the \(y\)-intercept.
Now suppose we want to find the equation of the line tangent to \(y=f(x)\) at \(x=a\). We know the slope is \(m=f'(a)\). So equation \((1)\) becomes: \[ y=f'(a)x+b \qquad (2) \] We know the line passes through the point \((x,y)=(a,f(a))\). So equation \((2)\) tell us: \[ f(a)=f'(a)a+b \] We solve for \(b\) and substitute back into \((2)\): \[\begin{aligned} b&=f(a)-f'(a)a \\[5pt] y&=f'(a)x+f(a)-f'(a)a\\ &=f(a)+f'(a)(x-a) \end{aligned}\] Using this formula for \(b\), equation \((2)\) becomes: \[\begin{aligned} y&=f'(a)x+f(a)-f'(a)a\\ &=f(a)+f'(a)(x-a) \end{aligned}\] which is the equation for the tangent line. We define the formula on the right to be the tangent function: \[ f_{\tan}(x)=f(a)+f'(a)(x-a) \] so that the equation of the tangent line is \(y=f_{\tan}(x)\).
The equation of the tangent line to the graph of the function \(y=f(x)\) at \(x=a\) is: \[ y=f_{\tan}(x) \equiv f(a)+f'(a)(x-a) \] In differential notation, this is: \[ y=f_{\tan}(x) \equiv f(a)+\left.\dfrac{df}{dx}\right|_{x=a}(x-a) \]
Memorize this!
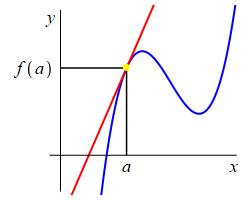
The equation of a tangent line can also be derived from the point-slope equation for a line. The slope is \[ m=\dfrac{y-y_o}{x-x_o} \] where \(m\) is the slope, \((x_o,y_o)\) is some point on the line and \((x,y)\) is a general point on the line. Solving for \(y\), the point-slope equation for the line is: \[ y=y_o+m(x-x_o) \] For the tangent line to \(f(x)\) at \(x=a\), the slope is \(m=f'(a)\) and \((x_o,y_o)=(a,f(a)\). So the point-slope equation becomes \[ y=f(a)+f'(a)(x-a) \]
Compute the tangent line to \(y=6x^2-x^3\) at \(x=3\). Then find its \(y\)-intercept. Its slope was found in an exercise on the previous page.
The solution is straightforward: find the required information and plug into the formula for the equation of the tangent line. We identify \(f(x)=6x^2-x^3\) and \(a=3\). Then: \[ f(3)=54-27=27 \] and from the previous page: \[ f'(3)=9 \] So the equation of the tangent line is: \[\begin{aligned} y&=f(a)+f'(a)(x-a) \\ &=f(3)+f'(3)(x-3) \\ &=27+9(x-3) \\ &=9x \end{aligned}\] We identify the \(y\)-intercept as \(b=0\).
Compute the tangent line to \(y=\dfrac{3}{x}\) at \(x=6\). Then find its \(y\)-intercept. Its derivative was found in an exercise on a previous page.
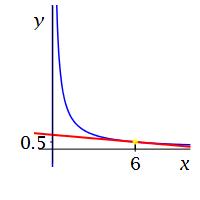
Evaluate the function and find its derivative at \(x=6\). Then use the formula: \[ f_{\tan}(x)=f(6)+f'(6)(x-6) \]
\(y=-\,\dfrac{1}{12}x+1\)
The \(y\)-intercept is \(b=1\).
We identify \(f(x)=\dfrac{3}{x}\) and \(a=6\). Then: \[ f(6)=\dfrac{1}{2} \] The derivative was found on a previous page to be: \[ f'(6)=-\,\dfrac{1}{12} \] So the equation of the tangent line is: \[\begin{aligned} y&=f(a)+f'(a)(x-a) \\ &=f(6)+f'(6)(x-6) \\ &=\dfrac{1}{2}-\dfrac{1}{12}(x-6) \\ &=-\,\dfrac{1}{12}x+1 \end{aligned}\] We identify the \(y\)-intercept as \(b=1\).
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum